Course for Mathematical Sciences
Theory of Numbers
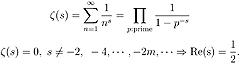
Riemann Hypothesis
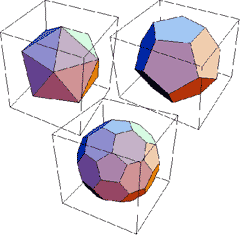
Regular and Quasi-Regular Polyhedrons
Tracing the Orbits of Moving Points
High school students learn about Newton's laws of dynamics that govern the movement of objects. Dynamics is the study of movements, called dynamical systems, which adhere to these established rules. For example, a recursive sequence can be represented as a series of points that follow a set rule, making its behavior a type of dynamical system. Specifically, suppose one was to examine the sequence (series of points) {xn} produced the recursive formula xn+1=axn(1?xn). Even a relatively straightforward recursive formula that is defined by a quadratic equation produces a sequence {xn} whose behavior is incredibly complex. Another mysterious and fascinating phenomenon is how the slightest adjustment to the fixed value a, or the initial value x0 can create entirely different behavior in the sequence. Figure 1 on the right is a computer rendering of the sequence when a=4 and x0=0.5. The intersections of the polygonal lines and diagonal line y = x correspond to the sequence {xn}, which meanders chaotically throughout the interval [0,1]. Meanwhile, the horizontal axis of Figure 2 shows values of a on the horizontal axis, and the values for {xn} on the vertical axis to illustrate the cluster points of the sequence. We can see that the cluster points become increasingly complex as the value of a increases from 0 to 4. Even high school-level mathematical concepts such as recursive formulas produce highly unpredictable behavior, making them useful subjects of study in the field of dynamical systems.
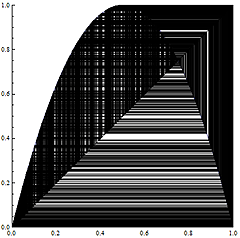 figure 1
figure 1 figure 2
figure 2Differential Geometry

Straight (geodesic) lines on spherical, flat, and curved (disc model) surfaces
We build on some mathematical models for phenomena by differential equations and study properties of their solutions to understand a kind of system sealed in nature.
We also derive some relationship between theory of numbers, geometry and differential equations, and find the mathematical structures there.

the Beat of a Drum Represented by Bessel Functions
It develops in connection with various branches of mathematics such as theory of numbers, differential equations, mathematical physics and cryptography.

Deformation of Quadratic Hyperboloids

Electron arrangement on a lattice (+spin connection components), percolation model
Representation Theory
Mathematics is often subdivided into the fields of algebra, geometry, and analysis. However, this distinction is ultimately artificial. Some aspects of mathematics simply cannot be so easily categorized. Representation theory is a unified methodology for the whole of mathematics, and how it is reckoned varies from researcher to researcher. Furthermore, the combinatorial phenomena and structures of representation theory itself are extraordinarily interesting and actively researched by modern mathematicians.

